Graphing Quadratics

This is a simple guide to graphing quadratics

A quadratic equation is most often given in one of two forms as shown below.

1. Standard form:  y = ax^2 + bx + c
2. Vertex form:  y=a(x-h)^2 + k

For the standard form ( y = ax^2 + bx + c) follow the steps below to graph

1. Find the vertex
1. Do -b/2a to find the x-coordinate of the vertex
2. Plug in the value from -b/2a into the original equation to solve for the y-coordinate of the vertex
3. Graph the vertex
2. Graph a point before and after the vertex
1. Choose an x-coordinate before the x-coordinate of the vertex
2. Plug this value into the original equation to find the value of the y-coordinate
3. Graph the point
4. Repeat a-c with an x-coordinate after the x-coordinate of the vertex

For the second form ( y=a(x-h)^2 + k) follow the steps below to graph

1. Find the vertex
1. The vertex is (h,k)
2. Graph the vertex
2. See step 2 from graphing a quadratic equation in standard form

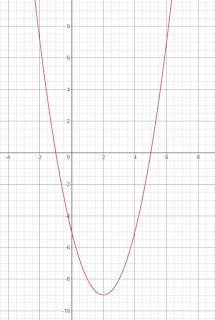
An example problem is y=x^2-4x-5

1. Find the vertex
1. X-coordinate is -b/2a = 4/(2(1)) = 2
2. Y-coordinate = 2^2 -4(2) - 5 = -9
3. The vertex is (2,-9)
2. Find a point before and after vertex
1. If x = 1, y = 1^2 - 4(1) - 5 = -8 so (1,-8)
2. If x = 3, y=3^2 -4(3) - 5 = (3,-8)
3. The final graph is shown